Reguła Naismitha
Reguła Naismitha – praktyczna zasada służąca do oszacowania czasu wędrówki. Została sformułowana w 1892 roku przez szkockiego alpinistę Williama W. Naismitha. Naismith podał ją w milach i stopach, współcześnie może być zdefiniowana na przykład tak:
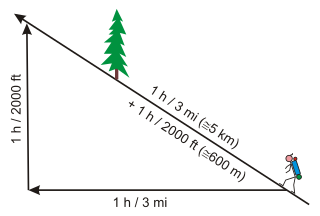
Przeznacz 1 godzinę na każde 3 mile (5 km) do przodu, plus 1 godzinę na każde 2000 stóp (600 m) w górę.
Reguła Naismitha
Oryginalna reguła Naismitha z 1892 roku mówi, że mężczyźni powinni przeznaczyć 1 godzinę na 3 mile na mapie i dodatkową 1 godzinę na 2000 stóp wzniesienia terenu. Jest ona zawarta w jednym, ostatnim zdaniu jego raportu z wycieczki w góry. William W. Naismith był szkockim alpinistą.
Współcześnie jest formułowana na różne sposoby – 1 h / 3 mi + 1 h / 2000 ft Naismitha mogą być zastąpione na:
- 1 h / 3 mi (5 km) + 1 h / 2000 ft (600 m)
- 1 h / 5 km (3 mi) + 1/2 h / 300 m (1000 ft)
- 12 min / 1 km + 10 min / 100 m
Reguła Naismitha (choć nie z nazwy) pojawia się w prawie brytyjskim. Jednym z rodzajów aktywności, których dostarczanie wymaga licencji jest trekking. Częścią jego definicji jest zastrzeżenie, że musi odbywać się na terenie, z którego droga lub schronienie mogą zostać osiągnięte w czasie dłuższym niż 30 minut przy prędkości 5 km / h plus jedna minuta na każde 10 metrów wzniesienia terenu.
Równowartość dystansu i różnicy wysokości Scarfa
W 1998 roku Scarf zaproponował uogólnienie reguły Naismitha, polegające na wprowadzeniu równowartości dystansu i różnicy wysokości. Według tego autora reguła Naismitha implikuje, że 2000 stóp różnicy wysokości odpowiada dystansowi 3 mil (=15840 stóp), ponieważ na przebycie każdego z tych odcinków potrzeba tyle samo czasu (jedną godzinę). W związku z tym Scarf wprowadził współczynnik:
który nazwał liczbą Naismitha. Przy takich założeniach:
- równoważny dystans = x + α·y
gdzie:
- x = dystans w poziomie
- y = dystans w pionie
Na przykład dla dystansu na mapie 15 km i różnicy wysokości 500 m
- równoważny dystans = 15 km + 7,92·0,5 km = 15 km + 3,96 km = 18,96 km.
Przy prędkości 5 km/h czas potrzebny na przebycie 15 km w poziomie i 500 m w pionie jest więc równy
- 18,96 km / 5 km/h = 3,792 h = 3 h 47,52 min
Jak widać, założenie Scarfa pozwala również obliczyć czas dla każdej prędkości, a nie tylko jednej jak w przypadku oryginalnej reguły Naismitha.
Tempo
Tempo (ang. pace) czyli odwrotność prędkości może być obliczone tutaj z następującego wzoru:
- p = p0·(1 + α·m)
gdzie:
- p = tempo
- p0 = tempo na płaskiej powierzchni
- m = gradient pod górę
Przykładowe obliczenia: p0 = 12 min / h (dla prędkości 5 km / h), m = 0.6 km w pionie / 5 km dystansu = 0.12, p = 12 · (1 + 7.92 · 0.12) = 23.4 min / km.
Inne modyfikacje
Poprawki Trantera
Tranter wprowadza poprawki na kondycję, niesiony ładunek, rodzaj gruntu po którym idzie się, pogodę. W celu ich zastosowania należy wcześniej określić swój poziom kondycji, czyli zmierzony w minutach czas przejścia pod górę dystansu 800 metrów w poziomie przy różnicy wysokości równej 300 metrów. Od poziomu kondycji można potem odjąć poprawki na niesiony ciężar, rodzaj podłoża po którym idzie się i wiatr. Czas obliczony na podstawie reguły Naismitha oraz tak wyznaczony poziom kondycji są następnie używane do odczytania czasu ze specjalnej tabeli.
Poprawki Aitkena
Aitken w 1977 roku podaje nie jeden jak Naismith, ale dwa dystanse, których przejście zajmuje 1 godzinę:
W każdym terenie 1 godzinę zajmuje pokonanie różnicy wysokości:
Aitken nie stosuje więc równowartości dystansu i różnicy wysokości (zaproponowanej w 1998 roku przez Scarfa).
Poprawki Langmuira
Langmuir rozszerza regułę na schodzenie w dół:
- minus 10 min na każde 300 m różnicy wysokości dla stoków o nachyleniu między 5 i 12 stopni
- plus 10 min na każde 300 m różnicy wysokości dla stoków o nachyleniu większym niż 12 stopni